CryptoDB
He Gives C-Sieves on the CSIDH
| Authors: |
- Chris Peikert , University of Michigan
|
| Download: |
- DOI: 10.1007/978-3-030-45724-2_16
(login may be required)
- Search ePrint
- Search Google
|
|
Conference:
|
EUROCRYPT 2020
|
| Abstract: |
Recently, Castryck, Lange, Martindale, Panny, and Renes proposed
\emph{CSIDH} (pronounced ``sea-side'') as a candidate post-quantum
``commutative group action.'' It has attracted much attention and
interest, in part because it enables noninteractive
Diffie--Hellman-like key exchange with quite small
communication. Subsequently, CSIDH has also been used as a foundation
for digital signatures.
In 2003--04, Kuperberg and then Regev gave asymptotically
subexponential quantum algorithms for ``hidden shift'' problems, which
can be used to recover the CSIDH secret key from a public key. In
late 2011, Kuperberg gave a follow-up quantum algorithm called the
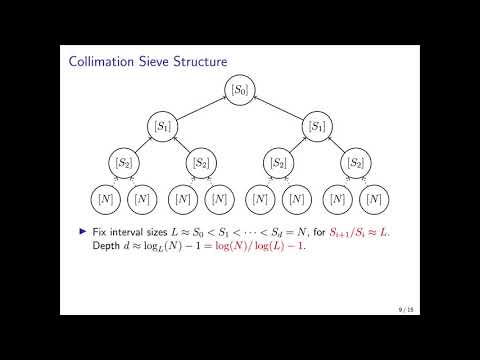
\emph{collimation sieve} (``c-sieve'' for short), which improves the
prior ones, in particular by using exponentially less quantum memory
and offering more parameter tradeoffs. While recent works have
analyzed the concrete cost of the original algorithms (and variants)
against CSIDH, nothing of this nature was previously available for the
c-sieve.
This work fills that gap. Specifically, we generalize Kuperberg's
collimation sieve to work for arbitrary finite cyclic groups, provide
some practical efficiency improvements, give a classical (i.e.,
non-quantum) simulator, run experiments for a wide range of parameters
up to the actual CSIDH-512 group order, and concretely quantify the
complexity of the c-sieve against CSIDH.
Our main conclusion is that the proposed CSIDH parameters provide
relatively little quantum security beyond what is given by the cost of
quantumly evaluating the CSIDH group action itself (on a uniform
superposition). For example, the cost of CSIDH-512 key recovery is
only about~$2^{16}$ quantum evaluations using~$2^{40}$ bits of
quantumly accessible \emph{classical} memory (plus relatively small
other resources). This improves upon a prior estimate of~$2^{32.5}$
evaluations and~$2^{31}$ qubits of \emph{quantum} memory, for a
variant of Kuperberg's original sieve.
Under the plausible assumption that quantum evaluation does not cost
much more than what is given by a recent ``best case'' analysis,
CSIDH-512 can therefore be broken using significantly less
than~$2^{64}$ quantum T-gates. This strongly invalidates its claimed
NIST level~1 quantum security, especially when accounting for the
MAXDEPTH restriction. Moreover, under analogous assumptions for
CSIDH-1024 and -1792, which target higher NIST security levels, except
near the high end of the MAXDEPTH range even these instantiations fall
short of level~1. |
Video from EUROCRYPT 2020
BibTeX
@inproceedings{eurocrypt-2020-30240,
title={He Gives C-Sieves on the CSIDH},
booktitle={39th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, May 10–14, 2020, Proceedings},
series={Lecture Notes in Computer Science},
publisher={Springer},
keywords={CSIDH;isogenies;post-quantum;cryptanalysis;hidden-shift problem;Kuperberg's algorithm},
volume={12105},
doi={10.1007/978-3-030-45724-2_16},
author={Chris Peikert},
year=2020
}