CryptoDB
Verifiable Random Functions with Optimal Tightness
| Authors: | |
|---|---|
| Download: | |
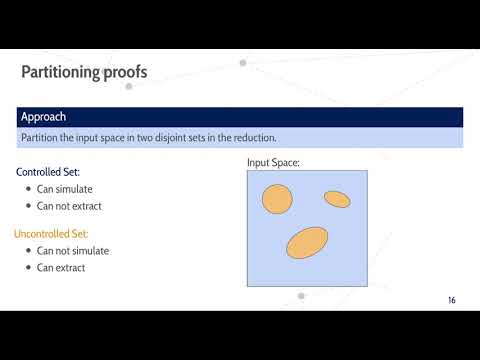
| Abstract: | Verifiable random functions (VRFs), introduced by Micali, Rabin and Vadhan (FOCS’99), are the public-key equivalent of pseudo- random functions. A public verification key and proofs accompanying the output enable all parties to verify the correctness of the output. How- ever, all known standard model VRFs have a reduction loss that is much worse than what one would expect from known optimal constructions of closely related primitives like unique signatures. We show that: 1. Every security proof for a VRF has to lose a factor of Q, where Q is the number of adversarial queries. To that end, we extend the meta- reduction technique of Bader et al. (EUROCRYPT’16) to also cover VRFs. 2. This raises the question: Is this bound optimal? We answer this question in the affirmative by presenting the first VRF that achieves this tightness. We thus paint a complete picture of the achievability of tight verifiable random functions: We show that a security loss of Q is unavoidable and present the first construction that achieves this bound. |
Video from PKC 2021
BibTeX
@article{pkc-2021-31000,
title={Verifiable Random Functions with Optimal Tightness},
booktitle={Public-Key Cryptography - PKC 2021},
publisher={Springer},
doi={10.1007/978-3-030-75248-4_3},
author={David Niehues},
year=2021
}