CryptoDB
Covert Learning: How to Learn with an Untrusted Intermediary
| Authors: | |
|---|---|
| Download: | |
| Presentation: | Slides |
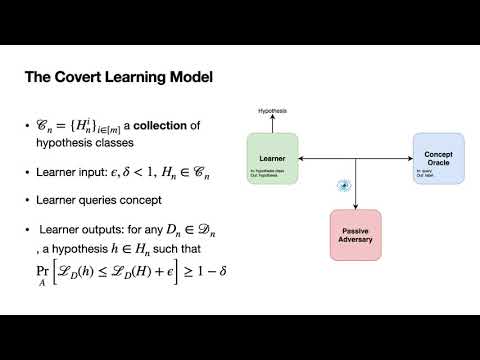
| Abstract: | We consider the task of learning a function via oracle queries, where the queries and responses are monitored (and perhaps also modified) by an untrusted intermediary. Our goal is twofold: First, we would like to prevent the intermediary from gaining any information about either the function or the learner's intentions (e.g. the particular hypothesis class the learner is considering). Second, we would like to curb the intermediary's ability to meaningfully interfere with the learning process, even when it can modify the oracles' responses. Inspired by the works of Ishai et al. (Crypto 2019) and Goldwasser et al. (ITCS 2021), we formalize two new learning models, called Covert Learning and Covert Verifiable Learning, that capture these goals. Then, assuming hardness of the Learning Parity with Noise (LPN) problem, we show: 1. Covert Learning algorithms in the agnostic setting for parity functions and decision trees, where a polynomial time eavesdropping adversary that observes all queries and responses learns nothing about either the function, or the learned hypothesis. 2. Covert Verifiable Learning algorithms that provide similar learning and privacy guarantees, even in the presence of a polynomial-time adversarial intermediary that can modify all oracle responses. Here the learner is granted additional random examples and is allowed to abort whenever the oracles responses are modified. Aside theoretical interest, our study is motivated by applications to the secure outsourcing of automated scientific discovery in drug design and molecular biology. It also uncovers limitations of current techniques for defending against model extraction attacks. |
Video from TCC 2021
BibTeX
@article{tcc-2021-31564,
title={Covert Learning: How to Learn with an Untrusted Intermediary},
booktitle={Theory of Cryptography;19th International Conference},
publisher={Springer},
doi={10.1007/978-3-030-90456-2_1},
author={Ran Canetti and Ari Karchmer},
year=2021
}