CryptoDB
Rational isogenies from irrational endomorphisms
| Authors: |
|
|---|---|
| Download: |
|
| Conference: | EUROCRYPT 2020 |
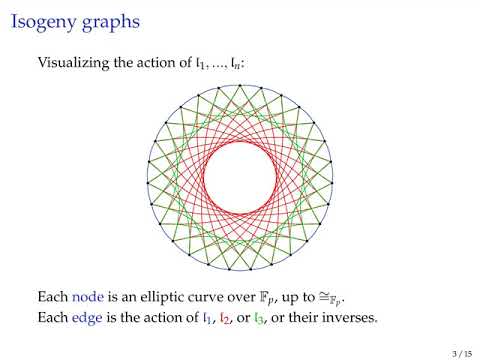
| Abstract: | In this paper, we introduce a polynomial-time algorithm to compute a connecting $\mathcal{O}$-ideal between two supersingular elliptic curves over $\mathbb{F}_p$ with common $\mathbb{F}_p$-endomorphism ring $\mathcal{O}$, given a description of their full endomorphism rings. This algorithm provides a reduction of the security of the CSIDH cryptosystem to the problem of computing endomorphism rings of supersingular elliptic curves. A similar reduction for SIDH appeared at Asiacrypt 2016, but relies on totally different techniques. Furthermore, we also show that any supersingular elliptic curve constructed using the complex-multiplication method can be located precisely in the supersingular isogeny graph by explicitly deriving a path to a known base curve. This result prohibits the use of such curves as a building block for a hash function into the supersingular isogeny graph. |
Video from EUROCRYPT 2020
BibTeX
@inproceedings{eurocrypt-2020-30243,
title={Rational isogenies from irrational endomorphisms},
booktitle={39th Annual International Conference on the Theory and Applications of Cryptographic Techniques, Zagreb, Croatia, May 10–14, 2020, Proceedings},
series={Lecture Notes in Computer Science},
publisher={Springer},
keywords={isogeny-based cryptography;endomorphism rings;CSIDH},
volume={12105},
doi={10.1007/978-3-030-45724-2_18},
author={Wouter Castryck and Lorenz Panny and Frederik Vercauteren},
year=2020
}