CryptoDB
Multi-Client Functional Encryption for Separable Functions
| Authors: | |
|---|---|
| Download: | |
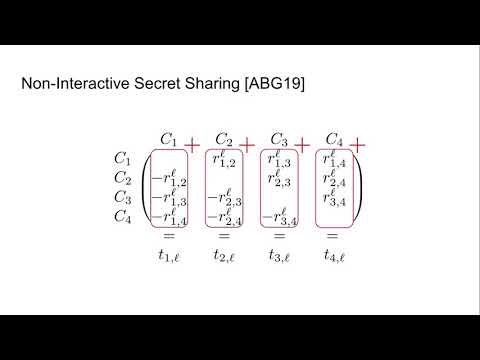
| Abstract: | In this work, we provide a compiler that transforms a single-input functional encryption scheme for the class of polynomially bounded circuits into a multi-client functional encryption (MCFE) scheme for the class of separable functions. An $n$-input function $f$ is called separable if it can be described as a list of polynomially bounded circuits $f^1,..., f^n$ s.t. $f(x_1,..., x_n)= f^1(x_1)+ ... + f^n(x_n)$ for all $x_1,..., x_n$. Our compiler extends the works of Brakerski et al. [Eurocrypt 2016] and of Komargodski et al. [Eurocrypt 2017] in which a generic compiler is proposed to obtain multi-input functional encryption (MIFE) from single-input functional encryption. Our construction achieves the stronger notion of MCFE but for the less generic class of separable functions. Prior to our work, a long line of results has been proposed in the setting of MCFE for the inner-product functionality, which is a special case of a separable function. We also propose a modified version of the notion of decentralized MCFE introduced by Chotard et al. [Asiacrypt 2018] that we call outsourceable mulit-client functional encryption (OMCFE). Intuitively, the notion of OMCFE makes it possible to distribute the load of the decryption procedure among at most $n$ different entities, which will return decryption shares that can be combined (e.g., additively) thus obtaining the output of the computation. This notion is especially useful in the case of a very resource consuming decryption procedure, while the combine algorithm is non-time consuming. We also show how to extend the presented MCFE protocol to obtain an OMCFE scheme for the same functionality class. |
Video from PKC 2021
BibTeX
@article{pkc-2021-30995,
title={Multi-Client Functional Encryption for Separable Functions},
booktitle={Public-Key Cryptography - PKC 2021},
publisher={Springer},
doi={10.1007/978-3-030-75245-3_26},
author={Michele Ciampi and Luisa Siniscalchi and Hendrik Waldner},
year=2021
}