CryptoDB
Targeted Lossy Functions and Applications
| Authors: |
|
|---|---|
| Download: |
|
| Conference: | CRYPTO 2021 |
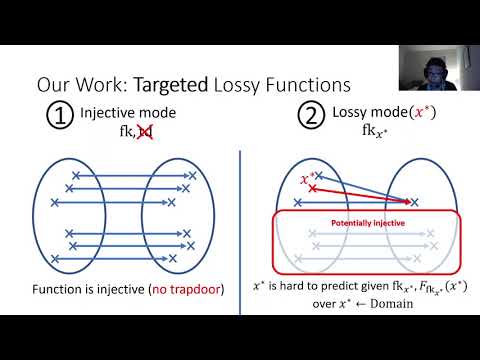
| Abstract: | Lossy trapdoor functions, introduced by Peikert and Waters (STOC '08), can be initialized in one of two indistinguishable modes: in injective mode, the function preserves all information about its input, and can be efficiently inverted given a trapdoor, while in lossy mode, the function loses some information about its input. Such functions have found countless applications in cryptography, and can be constructed from a variety of Cryptomania assumptions. In this work, we introduce \emph{targeted lossy functions (TLFs)}, which relax lossy trapdoor functions along two orthogonal dimensions. Firstly, they do not require an inversion trapdoor in injective mode. Secondly, the lossy mode of the function is initialized with some target input, and the function is only required to lose information about this particular target. The injective and lossy modes should be indistinguishable even given the target. We construct TLFs from Minicrypt assumptions, namely, injective pseudorandom generators, or even one-way functions under a natural relaxation of injectivity. We then generalize TLFs to incorporate \emph{branches}, and construct \emph{all-injective-but-one} and \emph{all-lossy-but-one} variants. We show a wide variety of applications of targeted lossy functions. In several cases, we get the first Minicrypt constructions of primitives that were previously only known under Cryptomania assumptions. Our applications include: \begin{itemize} \item \emph{Pseudo-entropy functions} from one-way functions. \item Deterministic leakage-resilient message-authentication codes and improved leakage-resilient symmetric-key encryption from one-way functions. \item Extractors for \emph{extractor-dependent sources} from one-way functions. \item Selective-opening secure symmetric-key encryption from one-way functions. \item A new construction of CCA PKE from (exponentially secure) trapdoor functions and injective pseudorandom generators. \end{itemize} We also discuss a fascinating connection to distributed point functions. |
Video from CRYPTO 2021
BibTeX
@inproceedings{crypto-2021-31226,
title={Targeted Lossy Functions and Applications},
publisher={Springer-Verlag},
doi={10.1007/978-3-030-84259-8_15},
author={Willy Quach and Brent Waters and Daniel Wichs},
year=2021
}