CryptoDB
Massive Superpoly Recovery with Nested Monomial Predictions
| Authors: |
|
|---|---|
| Download: | |
| Conference: | ASIACRYPT 2021 |
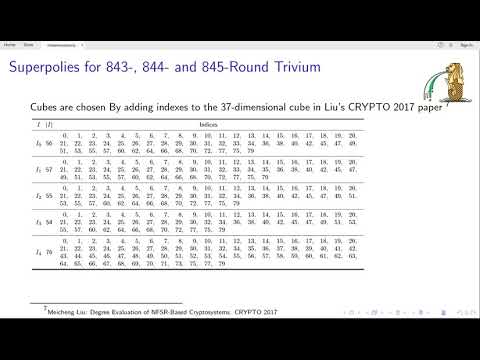
| Abstract: | Determining the exact algebraic structure or some partial information of the superpoly for a given cube is a necessary step in the cube attack -- a generic cryptanalytic technique for symmetric-key primitives with some secret and public tweakable inputs. Currently, the division property based approach is the most powerful tool for exact superpoly recovery. However, as the algebraic normal form (ANF) of the targeted output bit gets increasingly complicated as the number of rounds grows, existing methods for superpoly recovery quickly hit their bottlenecks. For example, previous method stuck at round 842, 190, and 892 for \trivium, \grain, and \kreyvium, respectively. In this paper, we propose a new framework for recovering the exact ANFs of massive superpolies based on the monomial prediction technique (ASIACRYPT 2020, an alternative language for the division property). In this framework, the targeted output bit is first expressed as a polynomial of the bits of some intermediate states. For each term appearing in the polynomial, the monomial prediction technique is applied to determine its superpoly if the corresponding MILP model can be solved within a preset time limit. Terms unresolved within the time limit are further expanded as polynomials of the bits of some deeper intermediate states with symbolic computation, whose terms are again processed with monomial predictions. The above procedure is iterated until all terms are resolved. Finally, all the sub-superpolies are collected and assembled into the superpoly of the targeted bit. We apply the new framework to \trivium, \grain, and \kreyvium. As a result, the exact ANFs of the superpolies for 843-, 844- and 845-round \trivium, 191-round \grain and 894-round \kreyvium are recovered. Moreover, with help of the M\"{o}bius transform, we present a novel key-recovery technique based on superpolies involving \textit{all} key bits by exploiting the sparse structures, which leads to the best key-recovery attacks on the targets considered. |
Video from ASIACRYPT 2021
BibTeX
@inproceedings{asiacrypt-2021-31491,
title={Massive Superpoly Recovery with Nested Monomial Predictions},
publisher={Springer-Verlag},
doi={10.1007/978-3-030-92062-3_14},
author={Kai Hu and Siwei Sun and Yosuke Todo and Meiqin Wang and Qingju Wang},
year=2021
}