CryptoDB
Reusable Two-Round MPC from LPN
| Authors: |
|
|---|---|
| Download: | |
| Conference: | PKC 2022 |
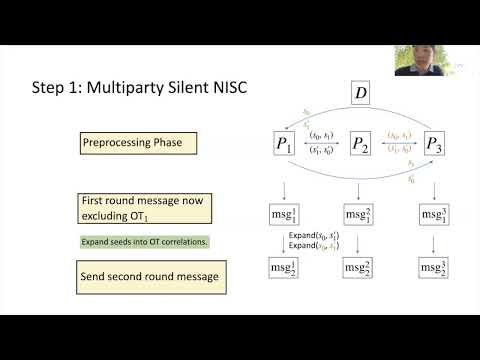
| Abstract: | We present a new construction of maliciously-secure, two-round multiparty computation (MPC) in the CRS model, where the first message is reusable an unbounded number of times. The security of the protocol relies on the Learning Parity with Noise (LPN) assumption with inverse polynomial noise rate $1/n^{1-\epsilon}$ for small enough constant $\epsilon$, where $n$ is the LPN dimension. Prior works on reusable two-round MPC required assumptions such as DDH or LWE that imply some flavor of homomorphic computation. We obtain our result in two steps: - In the first step, we construct a two-round MPC protocol in the {\it silent pre-processing model} (Boyle et al., Crypto 2019). Specifically, the parties engage in a computationally inexpensive setup procedure that generates some correlated random strings. Then, the parties commit to their inputs. Finally, each party sends a message depending on the function to be computed, and these messages can be decoded to obtain the output. Crucially, the complexity of the pre-processing phase and the input commitment phase do not grow with the size of the circuit to be computed. We call this {\it multiparty silent NISC} (msNISC), generalizing the notion of two-party silent NISC of Boyle et al. (CCS 2019). We provide a construction of msNISC from LPN in the random oracle model. - In the second step, we give a transformation that removes the pre-processing phase and use of random oracle from the previous protocol. This transformation additionally adds (unbounded) reusability of the first round message, giving the first construction of reusable two-round MPC from the LPN assumption. This step makes novel use of randomized encoding of circuits (Applebaum et al., FOCS 2004) and a variant of the ``tree of MPC messages" technique of Ananth et al. and Bartusek et al. (TCC 2020). |
Video from PKC 2022
BibTeX
@inproceedings{pkc-2022-31714,
title={Reusable Two-Round MPC from LPN},
publisher={Springer-Verlag},
author={James Bartusek and Akshayaram Srinivasan and Sanjam Garg and Yinuo Zhang},
year=2022
}