CryptoDB
Sine Series Approximation of the Mod Function for Bootstrapping of Approximate HE
| Authors: |
|
|---|---|
| Download: | |
| Presentation: | Slides |
| Conference: | EUROCRYPT 2022 |
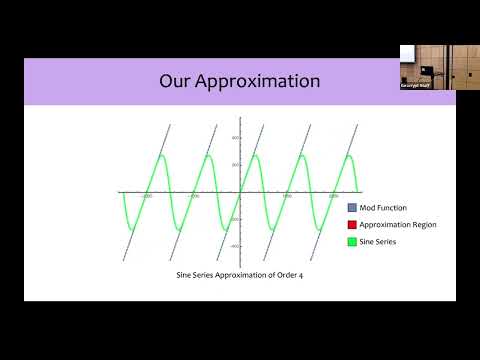
| Abstract: | While it is well known that the sawtooth function has a point-wise convergent Fourier series, the rate of convergence is not the best possible for the application of approximating the mod function in small intervals around multiples of the modulus. We show a different sine series, such that the sine series of order $n$ has error $O(\epsilon^{2n+1})$ for approximating the mod function in $\epsilon$-sized intervals around multiples of the modulus. Moreover, the resulting polynomial, after Taylor series approximation of the sine function, has small coefficients, and the whole polynomial can be computed at a precision that is only slightly larger than $-(2n+1)\log \epsilon$, the precision of approximation being sought. This polynomial can then be used to approximate the mod function to almost arbitrary precision, and hence allows practical CKKS-HE bootstrapping with arbitrary precision. We validate our approach by an implementation and obtain $100$ bit precision bootstrapping as well as improvements over prior work even at lower precision. |
Video from EUROCRYPT 2022
BibTeX
@inproceedings{eurocrypt-2022-31844,
title={Sine Series Approximation of the Mod Function for Bootstrapping of Approximate HE},
publisher={Springer-Verlag},
author={Charanjit S. Jutla and Nathan Manohar},
year=2022
}