CryptoDB
Lower Bound on SNARGs in the Random Oracle Model
| Authors: |
|
|---|---|
| Download: | |
| Presentation: | Slides |
| Conference: | CRYPTO 2022 |
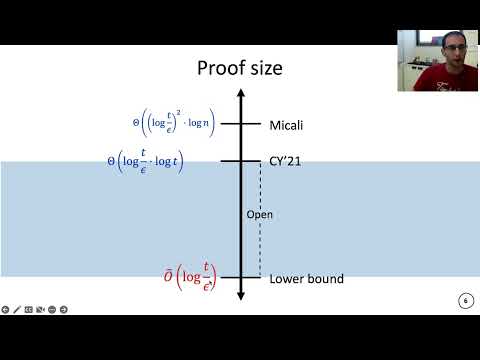
| Abstract: | Succinct non-interactive arguments (SNARGs) have become a fundamental primitive in the cryptographic community. The focus of this work is constructions of SNARGs in the Random Oracle Model (ROM). Such SNARGs enjoy post-quantum security and can be deployed using lightweight cryptography to heuristically instantiate the random oracle. A ROM-SNARG is \emph{$(t,\varepsilon)$-sound} if no $t$-query malicious prover can convince the verifier to accept a false statement with probability larger than $\varepsilon$. Recently, Chiesa-Yogev (CRYPTO '21) presented a ROM-SNARG of length ${\Theta}(\log (t/\varepsilon) \cdot \log t)$ (ignoring $\log n$ factors, for $n$ being the instance size). This improvement, however, is still far from the (folklore) lower bound of $\Omega(\log (t/\varepsilon))$. Assuming the \textit{randomized exponential-time hypothesis}, we prove a tight lower bound of ${\Omega}(\log (t/\varepsilon) \cdot \log t)$ for the length of {$(t,\varepsilon)$-sound} ROM-SNARGs. Our lower bound holds for constructions with non-adaptive verifiers and strong soundness notion called \textit{salted soundness}, restrictions that hold for \emph{all} known constructions (ignoring contrived counterexamples). We prove our lower bound by transforming any short ROM-SNARG (of the considered family) into a same length ROM-SNARG in which the verifier asks only a \emph{few} oracles queries, and then apply the recent lower bound of Chiesa-Yogev (TCC '20) for such SNARGs. |
Video from CRYPTO 2022
BibTeX
@inproceedings{crypto-2022-32126,
title={Lower Bound on SNARGs in the Random Oracle Model},
publisher={Springer-Verlag},
author={Eylon Yogev and Iftach Haitner and Daniel Nukrai},
year=2022
}