CryptoDB
On the Exact Round Complexity of Best-of-both-Worlds Multi-party Computation
| Authors: | |
|---|---|
| Download: | |
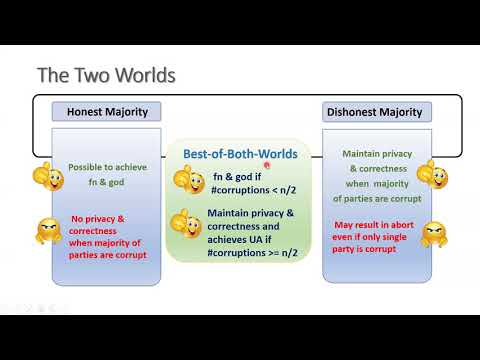
| Abstract: | The two traditional streams of multiparty computation (MPC) protocols consist of-- (a) protocols achieving guaranteed output delivery (\god) or fairness (\fair) in the honest-majority setting and (b) protocols achieving unanimous or selective abort (\uab, \sab) in the dishonest-majority setting. The favorable presence of honest majority amongst the participants is necessary to achieve the stronger notions of \god~or \fair. While the constructions of each type are abound in the literature, one class of protocols does not seem to withstand the threat model of the other. For instance, the honest-majority protocols do not guarantee privacy of the inputs of the honest parties in the face of dishonest majority and likewise the dishonest-majority protocols cannot achieve $\god$ and $\fair$, tolerating even a single corruption, let alone dishonest minority. The promise of the unconventional yet much sought-after species of MPC, termed as `Best-of-Both-Worlds' (BoBW), is to offer the best possible security depending on the actual corruption scenario. This work nearly settles the exact round complexity of two classes of BoBW protocols differing on the security achieved in the honest-majority setting, namely $\god$ and $\fair$ respectively, under the assumption of no setup (plain model), public setup (CRS) and private setup (CRS + PKI or simply PKI). The former class necessarily requires the number of parties to be strictly more than the sum of the bounds of corruptions in the honest-majority and dishonest-majority setting, for a feasible solution to exist. Demoting the goal to the second-best attainable security in the honest-majority setting, the latter class needs no such restriction. Assuming a network with pair-wise private channels and a broadcast channel, we show that 5 and 3 rounds are necessary and sufficient for the class of BoBW MPC with $\fair$ under the assumption of `no setup' and `public and private setup' respectively. For the class of BoBW MPC with $\god$, we show necessity and sufficiency of 3 rounds for the public setup case and 2 rounds for the private setup case. In the no setup setting, we show the sufficiency of 5 rounds, while the known lower bound is 4. All our upper bounds are based on polynomial-time assumptions and assume black-box simulation. With distinct feasibility conditions, the classes differ in terms of the round requirement. The bounds are in some cases different and on a positive note at most one more, compared to the maximum of the needs of the honest-majority and dishonest-majority setting. Our results remain unaffected when security with abort and fairness are upgraded to their identifiable counterparts. |
Video from ASIACRYPT 2020
BibTeX
@article{asiacrypt-2020-30669,
title={On the Exact Round Complexity of Best-of-both-Worlds Multi-party Computation},
booktitle={Advances in Cryptology - ASIACRYPT 2020},
publisher={Springer},
doi={10.1007/978-3-030-64840-4_3},
author={Arpita Patra and Divya Ravi and Swati Singla},
year=2020
}