CryptoDB
Proofs for Inner Pairing Products and Applications
| Authors: |
|
|---|---|
| Download: | |
| Conference: | ASIACRYPT 2021 |
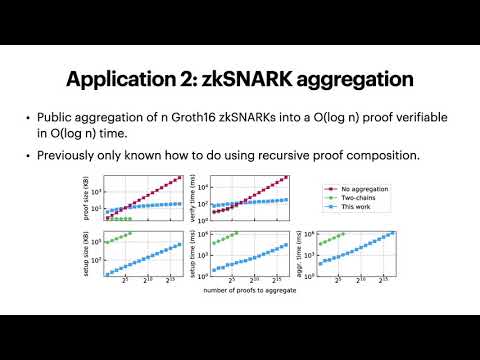
| Abstract: | We present a generalized inner product argument and demonstrate its applications to pairing-based languages. We apply our generalized argument to prove that an inner pairing product is correctly evaluated with respect to committed vectors of $n$ source group elements. With a structured reference string (SRS), we achieve a logarithmic-time verifier whose work is dominated by $6 \log n$ target group exponentiations. Proofs are of size $6 \log n$ target group elements, computed using $6n$ pairings and $4n$ exponentiations in each source group. We apply our inner product arguments to build the first polynomial commitment scheme with succinct (logarithmic) verification, $O(\sqrt{d})$ prover complexity for degree $d$ polynomials (not including the cost to evaluate the polynomial), and a SRS of size $O(\sqrt{d})$. Concretely, this means that for $d=2^{28}$, producing an evaluation proof in our protocol is $76\times$ faster than doing so in the KZG commitment scheme, and the CRS in our protocol is $1000\times$ smaller: $13$MB vs $13$GB for KZG. As a second application, we introduce an argument for aggregating $n$ Groth16 zkSNARKs into an $O(\log n)$ sized proof. Our protocol is significantly faster ($>1000\times$) than aggregating SNARKs via recursive composition: we aggregate $\sim 130,000$ proofs in $25$ minutes, versus $90$ proofs via recursive composition. Finally, we further apply our aggregation protocol to construct a low-memory SNARK for machine computations that does not rely on recursive composition. For a computation that requires time $T$ and space $S$, our SNARK produces proofs in space $\tilde{\mathcal{O}}(S+T)$, which is significantly more space efficient than a monolithic SNARK, which requires space $\tilde{\mathcal{O}}(S \cdot T)$. |
Video from ASIACRYPT 2021
BibTeX
@inproceedings{asiacrypt-2021-31438,
title={Proofs for Inner Pairing Products and Applications},
publisher={Springer-Verlag},
doi={10.1007/978-3-030-92078-4_3},
author={Benedikt Bünz and Mary Maller and Pratyush Mishra and Nirvan Tyagi and Psi Vesely},
year=2021
}