CryptoDB
Non-Malleable Secret Sharing against Bounded Joint-Tampering Attacks in the Plain Model
| Authors: |
|
|---|---|
| Download: |
|
| Presentation: | Slides |
| Conference: | CRYPTO 2020 |
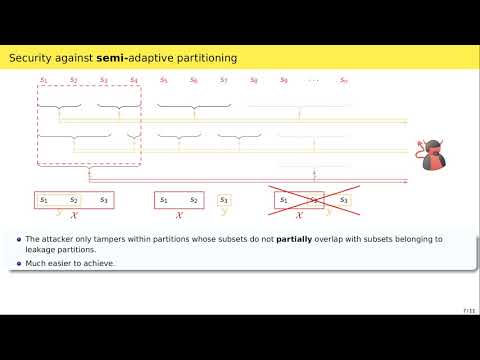
| Abstract: | Secret sharing enables a dealer to split a secret into a set of shares, in such a way that certain authorized subsets of share holders can reconstruct the secret, whereas all unauthorized subsets cannot. Non-malleable secret sharing (Goyal and Kumar, STOC 2018) additionally requires that, even if the shares have been tampered with, the reconstructed secret is either the original or a completely unrelated one. In this work, we construct non-malleable secret sharing tolerating $p$-time {\em joint-tampering} attacks in the plain model (in the computational setting), where the latter means that, for any $p>0$ fixed {\em a priori}, the attacker can tamper with the same target secret sharing up to $p$ times. In particular, assuming one-to-one one-way functions, we obtain: - A secret sharing scheme for threshold access structures which tolerates joint $p$-time tampering with subsets of the shares of maximal size ({\em i.e.}, matching the privacy threshold of the scheme). This holds in a model where the attacker commits to a partition of the shares into non-overlapping subsets, and keeps tampering jointly with the shares within such a partition (so-called {\em selective partitioning}). - A secret sharing scheme for general access structures which tolerates joint $p$-time tampering with subsets of the shares of size $O(\sqrt{\log n})$, where $n$ is the number of parties. This holds in a stronger model where the attacker is allowed to adaptively change the partition within each tampering query, under the restriction that once a subset of the shares has been tampered with jointly, that subset is always either tampered jointly or not modified by other tampering queries (so-called {\em semi-adaptive partitioning}). At the heart of our result for selective partitioning lies a new technique showing that every one-time {\em statistically} non-malleable secret sharing against joint tampering is in fact {\em leakage-resilient} non-malleable ({\em i.e.},\ the attacker can leak jointly from the shares prior to tampering). We believe this may be of independent interest, and in fact we show it implies lower bounds on the share size and randomness complexity of statistically non-malleable secret sharing against {\em independent} tampering. |
Video from CRYPTO 2020
BibTeX
@inproceedings{crypto-2020-30438,
title={Non-Malleable Secret Sharing against Bounded Joint-Tampering Attacks in the Plain Model},
publisher={Springer-Verlag},
doi={10.1007/978-3-030-56877-1_5},
author={Gianlunca Brian and Antonio Faonio and Maciej Obremski and Mark Simkin and Daniele Venturi},
year=2020
}